Congreve's
sponges
The sponge
problem of Sir W. Congreve, of rocket fame. Three horizontal rollers
are fixed in a frame; an endless band of sponge runs round these
rollers, and carries on the outside an endless chain of weights
surrounding the band of sponge and attached to it, so that they must
move together, every part of this band and chain being so accurately
uniform in weight that the perpendicular side will, in all positions of
band and chain be in equilibrium with the hypotenuse, on the principle
of the inclined plane.
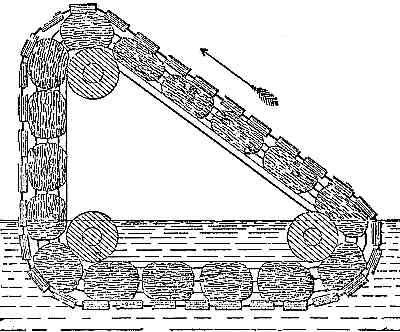
The frame in
which these rollers are fixed is placed in a cistern of water having
its lower part immersed. On the perpendicular side of the triangle, the
weights hanging
perpendicularly alongside the band of sponge, the band is not
compressed by them; and, its pores being left open, the water, at the
point where the band meets its surface, will rise to a certain height
above its level, and thereby create a load, which load will not exist
on the ascending side, because on this side the chain of weights
compresses the band at the water's edge, and squeezes out any water
that may have previously accumulated in it, so that the band rises in a
dry state, the weight of the chain having been so proportioned to the
breadth and thickness of the band as to be sufficient to produce this
effect.
(Subsection 945, from
p.378)
From: Gardner D. Hiscox, M.E., Mechanical Appliances and Novelties of Construction (1927), Norman W. Henley Publ. Co.






